Gate Equations Solving: A Comprehensive Guide to Mastering the Art

Introduction:

Gate equations solving is a fundamental concept in the field of digital electronics. It involves the process of finding the output values of logic gates based on the input values and the logical operations performed by the gates. By solving these equations, engineers and designers can analyze and predict the behavior of complex digital circuits. Gate equations solving plays a crucial role in the design and optimization of digital systems, ensuring their proper functioning and reliability.

Key Takeaways:

Gate Type	Input Combination	Output
AND	0, 0	0
AND	0, 1	0
AND	1, 0	0
AND	1, 1	1
OR	0, 0	0
OR	0, 1	1
OR	1, 0	1
OR	1, 1	1
NOT	0	1
NOT	1	0

(Note: The table above provides a concise summary of the input combinations and corresponding outputs for common gate types.)

Understanding Gate Equations

Simple adder on logic gates — Image by LISnapyc – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

Flip Flop logic circuit. — Image by Sommacal alfonso – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

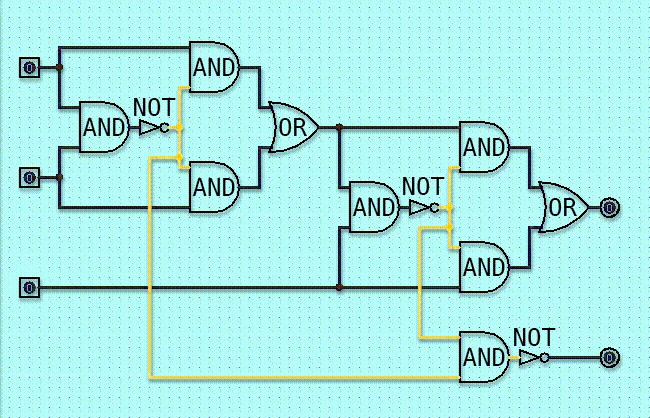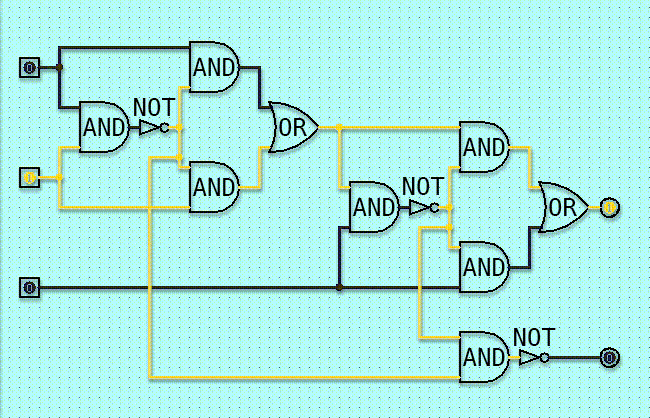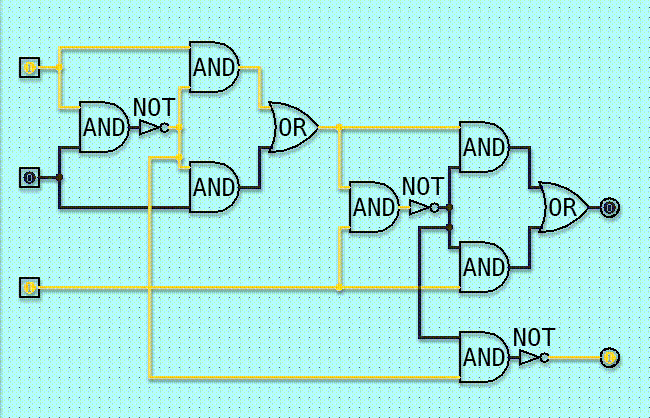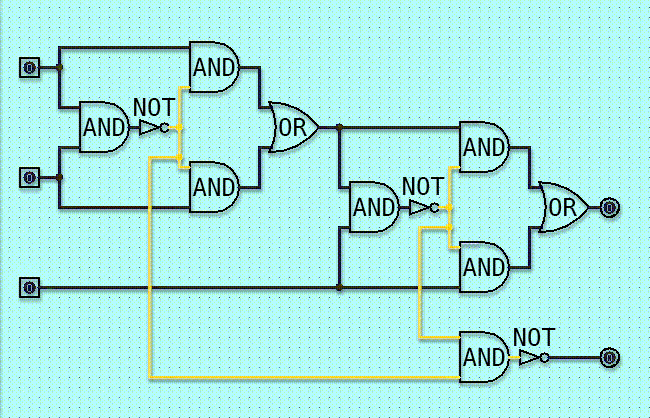
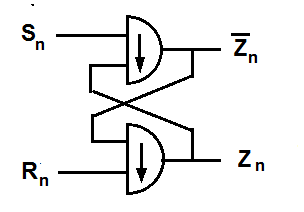
Gate equations play a crucial role in the field of electrical engineering and digital electronics. These equations are used to describe the behavior and characteristics of logic gates, which are fundamental building blocks of digital circuits. By understanding gate equations, engineers can analyze, optimize, and solve complex problems related to digital circuits.

Definition and Importance of Gate Equations

Gate equations can be defined as mathematical expressions that represent the relationship between the input and output signals of a logic gate. These equations are derived based on the underlying physics and principles of the gate‘s operation. They allow engineers to predict the behavior of a gate and determine its output for a given set of input conditions.

The importance of gate equations lies in their ability to provide insights into the functioning of digital circuits. By analyzing these equations, engineers can gain a deeper understanding of how logic gates process and manipulate binary signals. This knowledge is essential for designing and troubleshooting digital systems.

Solving gate equations involves finding the values of the output signals for a given set of input signals. This process requires applying various techniques and methods to simplify and manipulate the equations. Gate equation solvers, both manual and computer-based, are used to perform these calculations efficiently.

Practical Applications of Gate Equations

Gate equations find practical applications in various areas of electrical engineering and digital electronics. Some of the key applications include:

Logic Design: Gate equations are used in the design of digital circuits to determine the optimal arrangement of logic gates. By analyzing the equations, engineers can optimize the circuit’s performance, minimize power consumption, and ensure reliable operation.
Fault Diagnosis: Gate equations are valuable tools for diagnosing faults in digital circuits. By comparing the expected output values calculated from the equations with the actual measured values, engineers can identify and locate faulty components or connections.
Timing Analysis: Gate equations are used to analyze the timing characteristics of digital circuits. By considering the propagation delays and gate delays specified in the equations, engineers can ensure that the circuit meets the required timing constraints.
Power Optimization: Gate equations help in optimizing the power consumption of digital circuits. By analyzing the equations and considering factors such as gate capacitance and switching frequency, engineers can minimize power dissipation and improve energy efficiency.

Basics of Solving Equations

Solving equations is a fundamental skill in mathematics and plays a crucial role in various fields, including physics, engineering, and finance. It involves finding the values of variables that satisfy a given equation. In this section, we will explore two common methods for solving equations: algebraic methods and solving equation systems.

How to Solve Equations Algebraically

Algebraic methods involve manipulating equations using mathematical operations to isolate the variable and determine its value. Here are some key techniques and methods used in solving equations algebraically:

Inverse Operations: To isolate the variable, we perform inverse operations on both sides of the equation. For example, if we have the equation $2x + 5 = 15$ , we can subtract 5 from both sides to get $2x = 10$ . Then, dividing both sides by 2 gives us the solution $x = 5$ .
Combining Like Terms: In equations with multiple terms, we can simplify the equation by combining like terms. For instance, if we have the equation $3x + 2 - x = 7$ , we can combine the x terms to get $2x + 2 = 7$ . From there, we can proceed with the inverse operations to solve for x.
Factoring: Factoring involves expressing an equation as a product of its factors. By factoring, we can simplify complex equations and identify possible solutions. For example, if we have the equation $x^2 - 4 = 0$ , we can factor it as $(x + 2)(x - 2) = 0$ . This equation suggests that x can be either -2 or 2.
Quadratic Formula: The quadratic formula is a powerful tool for solving quadratic equations of the form $ax^2 + bx + c = 0$ . It states that the solutions can be found using the formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ . By substituting the values of a, b, and c into the formula, we can determine the solutions.

How to Solve Equation Systems

Equation systems involve a set of equations with multiple variables. Solving equation systems requires finding values for all the variables that satisfy all the equations simultaneously. Here are some methods commonly used to solve equation systems:

Substitution Method: In the substitution method, we solve one equation for one variable and substitute that expression into the other equations. This process continues until we find the values for all variables. For example, consider the system of equations:
$2x + 3y = 10$
$x - 2y = 5$

We can solve the second equation for x as $x = 5 + 2y$ . Substituting this expression into the first equation gives us $2(5 + 2y) + 3y = 10$ . By simplifying and solving for y, we can then substitute the value of y back into the equation to find x.

Elimination Method: The elimination method involves adding or subtracting equations to eliminate one variable and solve for the other. This method is particularly useful when the coefficients of one variable in the equations are additive inverses. For example, consider the system of equations:
$2x + 3y = 10$
$4x - 6y = 20$

By multiplying the first equation by 2 and the second equation by -1, we can eliminate the x variable by adding the equations together. This results in $9y = 30$ , from which we can find the value of y. Substituting this value back into one of the original equations allows us to solve for x.

Matrix Method: The matrix method involves representing the equation system as a matrix and using matrix operations to solve for the variables. This method is particularly useful for larger systems of equations. By performing row operations on the matrix, such as row reduction or Gaussian elimination, we can transform it into a form where the solutions are easily determined.

Solving equations algebraically and solving equation systems are essential skills that allow us to find solutions to mathematical problems and real-world scenarios. By applying these techniques and methods, we can analyze, optimize, and understand the relationships between variables and parameters in various contexts.

Introduction to Gauss Method

The Gauss Method, also known as Gaussian Elimination, is a powerful mathematical technique used to solve systems of linear equations. It is named after the German mathematician Carl Friedrich Gauss, who developed the method in the early 19th century. This method is widely used in various fields, including engineering, physics, and computer science, to solve complex equations and analyze systems.

Overview of Gauss Elimination Method

The Gauss Elimination Method is a systematic approach to solving systems of linear equations. It involves transforming the given system into an equivalent system that is easier to solve. The method consists of three main steps:

Row Operations: The system of equations is represented as a matrix, and row operations are performed to simplify the matrix. These operations include swapping rows, multiplying rows by a constant, and adding or subtracting rows.
Row Echelon Form: The goal of row operations is to transform the matrix into row echelon form. In this form, the leading coefficient (the first non-zero entry) of each row is to the right of the leading coefficient of the row above it. This process helps in identifying the solutions of the system.
Back Substitution: Once the matrix is in row echelon form, back substitution is used to find the values of the variables. Starting from the bottom row, the values of the variables are determined by substituting the known values into the equations above.

The Gauss Elimination Method provides a systematic and efficient way to solve systems of linear equations. It simplifies complex equations and allows for easier analysis of systems.

How to Solve Gaussian Elimination

To solve a system of linear equations using Gaussian Elimination, follow these steps:

Write the system of equations in matrix form. For example, consider the following system:

2x + 3y - z = 7 4x - 2y + 2z = -4 -3x + 2y - 5z = 9

This system can be represented as the augmented matrix:

Perform row operations to transform the matrix into row echelon form. Apply operations such as swapping rows, multiplying rows by a constant, and adding or subtracting rows to simplify the matrix.
Once the matrix is in row echelon form, perform back substitution to find the values of the variables. Start from the bottom row and substitute the known values into the equations above.
Continue substituting the values until all variables are determined. The resulting values represent the solution to the system of equations.

Gaussian Elimination provides a systematic approach to solving systems of linear equations, making it easier to find solutions and analyze the relationships between variables.

Using Gauss Elimination Calculator

To simplify the process of solving systems of linear equations using Gaussian Elimination, you can use online Gauss Elimination calculators. These calculators allow you to input the coefficients of the equations and automatically perform the necessary calculations to find the solution.

By using a Gauss Elimination calculator, you can save time and effort in manually performing the row operations and back substitution. These calculators provide quick and accurate results, making them a valuable tool for solving complex systems of equations.

Deep Dive into Gauss-Jordan Elimination

Understanding Gauss-Jordan Elimination

Gauss-Jordan elimination is a powerful method used to solve systems of linear equations. It is an extension of the Gaussian elimination method, which is commonly used to reduce a matrix to its row-echelon form. The main difference between the two methods lies in the final step of Gauss-Jordan elimination, where the row-echelon form is further reduced to the reduced row-echelon form.

The goal of Gauss-Jordan elimination is to transform a matrix into a form where the leading coefficient of each row is 1, and all other entries in the same column are 0. This process allows us to easily solve systems of linear equations by representing them in matrix form.

To understand Gauss-Jordan elimination, let’s consider an example. Suppose we have the following system of equations:

2x + 3y - z = 7 x - y + 2z = -1 3x + 2y - 4z = 4

We can represent this system in matrix form as:

The first step in Gauss-Jordan elimination is to perform row operations to create zeros below the leading coefficient of each row. This is achieved by subtracting multiples of one row from another row. The goal is to create a triangular matrix, where all entries below the leading coefficient are zero.

Once we have a triangular matrix, we proceed to the second step of Gauss-Jordan elimination. In this step, we perform row operations to create zeros above the leading coefficient of each row. This is done by subtracting multiples of one row from another row. The end result is a reduced row-echelon form, where the leading coefficient of each row is 1 and all other entries in the same column are 0.

Differences between Gauss and Gauss-Jordan Elimination

While Gauss and Gauss-Jordan elimination methods share similarities, there are some key differences between them. The main difference lies in the final step of the elimination process.

In Gauss elimination, we stop once we have obtained a row-echelon form. This form is sufficient for solving systems of linear equations. However, it may not provide a unique solution. There can be multiple solutions or no solution at all, depending on the system of equations.

On the other hand, Gauss-Jordan elimination takes the elimination process one step further. It reduces the row-echelon form to the reduced row-echelon form. This form provides a unique solution to the system of equations, if it exists. If there are any free variables, they are represented by parameters in the solution.

How to Solve Gaussian Elimination Matrix using Gauss-Jordan Method

To solve a system of linear equations using Gauss-Jordan elimination, we follow these steps:

Write the system of equations in matrix form.
Perform row operations to create zeros below the leading coefficient of each row, resulting in a triangular matrix.
Perform row operations to create zeros above the leading coefficient of each row, resulting in the reduced row-echelon form.
Interpret the reduced row-echelon form to obtain the solution to the system of equations.

Let’s apply these steps to the example we discussed earlier:

Step 1: The system of equations is already in matrix form.

Step 2: Perform row operations to create zeros below the leading coefficient of each row. After performing the necessary row operations, we obtain the following triangular matrix:

Step 3: Perform row operations to create zeros above the leading coefficient of each row. After performing the necessary row operations, we obtain the following reduced row-echelon form:

Step 4: Interpret the reduced row-echelon form. The solution to the system of equations is x = -1, y = -1, and z can take any value.

By following these steps, we can solve systems of linear equations using the Gauss-Jordan elimination method. It provides a systematic approach to finding solutions and allows for efficient analysis and optimization of gate equations in various fields.

Gate-1 and Gate Solutions

Image by Pluke – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 3.0.

Introduction to Gate-1 in Gate Equations

Gate-1 is a crucial component in gate equations, which play a significant role in various fields such as mathematics, physics, and engineering. In gate equations, Gate-1 represents the initial condition or the starting point of the equation. It serves as a reference point from which the equation is solved or analyzed.

When dealing with gate equations, it is essential to understand the significance of Gate-1. It provides a baseline or a known value that helps in solving the equation. Gate-1 acts as a starting point for the analysis and allows for the exploration of different scenarios and outcomes.

Importance and Role of Gate Solutions in Solving Equations

Gate solutions are the key to solving gate equations effectively. They provide techniques, methods, and analysis tools to find the desired outcomes or solutions. Gate solutions help in optimizing the equation by manipulating variables and parameters to achieve the desired results.

One of the primary objectives of gate equation solvers is to find the optimal values for the variables involved. These solvers use various techniques, such as numerical methods, optimization algorithms, and analytical approaches, to determine the best possible solutions.

Gate equation solvers employ different strategies to analyze and solve complex equations. They may use iterative methods, linear algebra techniques, or numerical approximation methods to find the most accurate and efficient solutions. These solvers play a crucial role in various fields, including engineering design, scientific research, and mathematical modeling.

To better understand the importance of gate solutions, let’s consider an example. Suppose we have a gate equation that represents the growth rate of a population over time. By using gate equation techniques and methods, we can analyze the equation to determine the factors that influence population growth. We can manipulate the variables and parameters to optimize the growth rate and predict future population trends.

Frequently Asked Questions

1. How does the Gauss method help in solving equations?

The Gauss method, also known as Gaussian elimination, is a technique used to solve systems of linear equations. It involves transforming the system into an equivalent system that is easier to solve by eliminating variables. This method is particularly useful when dealing with large systems of equations.

2. What is the Gauss elimination method?

The Gauss elimination method, also referred to as Gaussian elimination, is an algorithm used to solve systems of linear equations. It involves performing a sequence of elementary row operations on the augmented matrix of the system to reduce it to row-echelon form or reduced row-echelon form, making it easier to solve.

3. How can I solve equations algebraically?

To solve equations algebraically, you can use various techniques such as substitution, elimination, or the Gauss elimination method. These methods involve manipulating the equations to isolate the variable you want to solve for and then solving for that variable.

4. What is the Gauss-Jordan elimination method?

The Gauss-Jordan elimination method is an extension of the Gauss elimination method. It involves performing row operations on the augmented matrix of a system of linear equations to transform it into reduced row-echelon form. This method provides a unique solution to the system, if one exists, or determines if the system is inconsistent or has infinitely many solutions.

5. Is there a calculator for Gauss elimination?

Yes, there are online calculators available that can perform Gauss elimination for you. These calculators take the augmented matrix of the system of equations as input and provide the solution or reduced row-echelon form as output. You can search for “Gauss elimination calculator” to find such tools.

6. How can I solve equation systems using Gauss elimination?

To solve equation systems using Gauss elimination, you need to represent the system of equations as an augmented matrix. Then, perform row operations on the matrix to reduce it to row-echelon form or reduced row-echelon form. Finally, interpret the resulting matrix to obtain the solution to the system of equations.

7. What is Gaussian elimination?

Gaussian elimination is another term for the Gauss elimination method. It is an algorithm used to solve systems of linear equations by transforming the augmented matrix of the system into row-echelon form or reduced row-echelon form. This method simplifies the process of solving systems of equations.

8. How can I solve a Gaussian elimination matrix?

To solve a Gaussian elimination matrix, you need to perform row operations on the matrix to reduce it to row-echelon form or reduced row-echelon form. These row operations include swapping rows, multiplying rows by constants, and adding or subtracting rows. Once the matrix is in the desired form, you can interpret it to obtain the solution to the system of equations.

9. What are gate equations and how can I solve them?

Gate equations refer to the mathematical equations that describe the behavior of logic gates in digital circuits. To solve gate equations, you can use techniques such as Boolean algebra, truth tables, or Karnaugh maps. These methods help simplify the equations and determine the output of the gate for different input combinations.

10. Are there specific techniques for optimizing gate equations?

Yes, there are techniques for optimizing gate equations in digital circuit design. Some common techniques include logic minimization, gate-level optimization, and technology mapping. These methods aim to reduce the number of gates, minimize propagation delays, and optimize power consumption in the circuit.

Also Read:

TechieScience Core SME

The TechieScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the TechieScience.com website.

All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.

techiescience.com